Tras el artículo que realizamos hace unos días sobre cómo detectar anomalías en el número de logins fallidos de una corporación aplicando modelos predictivos en base a series temporales, he decidido continuar por esa línea y aplicar una filosofía similar para otros artículos. En este artículo intentaremos detectar cuando un usuario hace login en un número de máquinas mayor de las que normalmente suele hacerlo. Esto es útil para detectar potenciales movimientos laterales dentro de una organización.

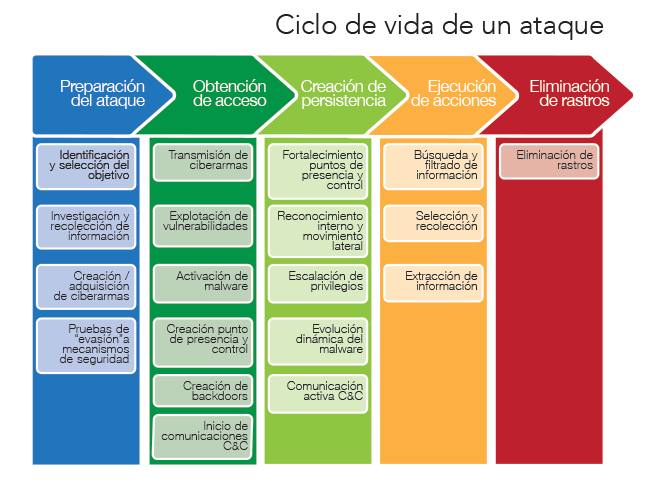
Cuando un usuario que normalmente hace login en 2 o 3 máquinas, por ejemplo, se está moviendo entre 10 o 15, puede suponer un posible movimiento lateral y eso no debería gustarnos mucho si somos los del BlueTeam.

¿Qué queremos hacer?

En este caso realizaremos una estimación estadística del número de logins exitosos en máquinas por cada uno de los usuarios de nuestra empresa. Si detectamos que ese número se incrementa de forma drástica respecto al estudio, generamos una alerta. Para ello usaremos otro método diferente al aplicado a series temporales. Los motivos principales son dos.

• Los modelos predictivos son costosos a nivel computacional y, si queremos realizar un modelo por cada usuario de nuestra organización, podemos matar a nuestro Search Head a base de cálculos. No es una opción viable.
• Se pueden exprimir otras opciones que ofrece Splunk para realizar este tipo de alertas.

Estadística básica para ciberseguridad

Antes de continuar con el artículo, vamos a realizar un pequeño tutorial básico sobre estadística. Nada complicado ni difícil, sólo para que tengáis una pequeña idea sobre cómo qué conceptos vamos a aplicar a este tipo de alertas.

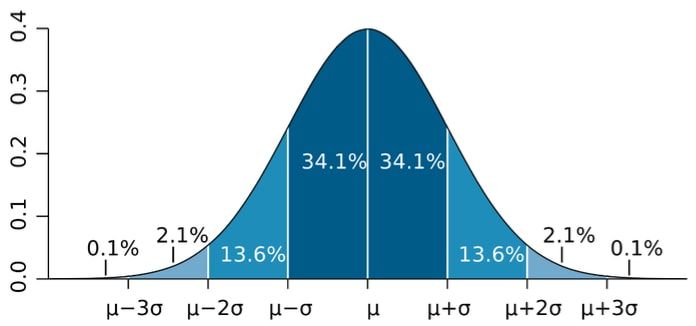
• Distribución normal o distribución de Gauss. Esta campana, conocida por todos los que hayan realizado algún curso básico de estadística, lo único que nos indica es cómo se distribuyen los datos. Los valores más repetidos quedan en la parte central de la campana y, a medida que nos movemos hacia los laterales, se irían representando los valores con menor número de ocurrencias en nuestro conjunto de datos.  Esto es, una distribución normal y su representación se hace mediante un histograma.

• El teorema de límite central. El teorema describe la distribución de la media de una muestra aleatoria proveniente de una población con varianza finita. Cuando el tamaño de la muestra es lo suficientemente grande, la distribución de las medias sigue aproximadamente una distribución normal. El teorema se aplica independientemente de la forma de la distribución de los datos.
• Desviación típica. Este concepto estipula que alrededor del 68% de los valores de una distribución normal están a una distancia σ < 1 (σ = desviación típica) de la media. Sobre el 95% de los valores se encuentra una distancia de 2σ del centro de la campana. Finalmente, el 99,7% de los valores se encuentra a una distancia del centro de la campana de 3σ. Esta sigma cambiará para cada conjunto de datos dado, en nuestro caso, para cada usuario de la organización. Tiene una fórmula matemática está descrita por:

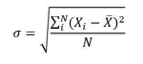
Donde σ es la desviación típica a hallar, x_i es la muestra actual /x es el valor medio de estas observaciones, y N es el número de observaciones de la muestra. Pero nos os preocupéis, todo esto lo hace Splunk internamente y no tendremos que andar con sumatorios ni demás desgracias matemáticas; bastará con aporrear el teclado de nuestro equipo con algo de talento jaja.

Todos estos conceptos son los que usaremos para determinar un comportamiento anómalo. En base a lo descrito, determinaremos en cuántas máquinas un usuario suele loggarse cada hora. Cuando detectemos que el número de máquinas en las que se loga es superior a 2σ, podremos decir con cierta seguridad que se está produciendo un comportamiento anómalo.

¿Qué tipo de datos nos interesa representar?

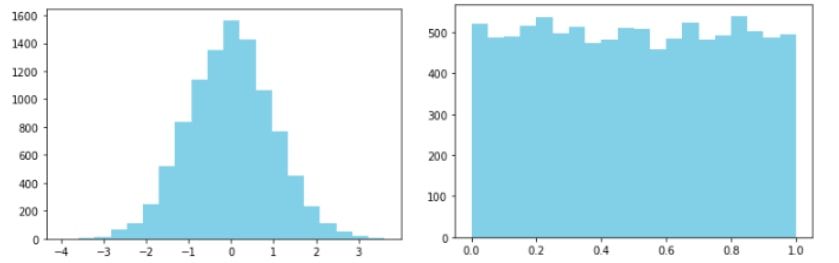
Como cabe esperar, los datos deben tener cierta distribución. No puede ser difusos ni estar homogéneamente distribuidos, es decir, no pueden no tener pinta de campana ya que si no es difícil determinar los límites del corte que aplicaremos para definir lo que es anómalo de lo que no lo es. En concreto, los datos deben tener pinta de distribución normal, forma de campana. Si los datos tienen forma de distribución uniforme, costará más determinar si los outlier son excepciones.

Lo que haremos será definir 2 veces σ como límite para detectar anomalías, o más bien la moda + 2 veces σ. Esto queda representado en el siguiente gráfico donde, si detectamos que el número de máquinas en las que un usuario ha hecho login es mayor al límite creado, podemos deducir que el comportamiento es raro. Este límite marcado con la flecha morada representa 2 veces la desviación típica o 2 σ, nuestro límite superior.

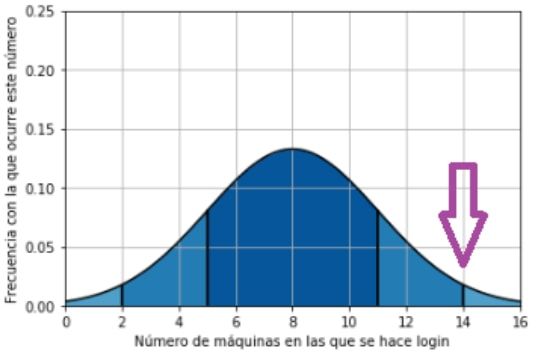
¿Movimientos laterales? ¿Alguien accediendo a sitios que no debe? Quedará en manos del analista de seguridad determinar esto.

Implementando alertas estadisticas en Splunk

Todo esto está muy bien, pero ¿cómo hago esto con Splunk? Deberíamos analizar el comportamiento de todos los usuarios y ver que, efectivamente, cumplen la propiedad descrita anteriormente. Es decir, modelar para cada usuario cuál es el número de máquinas en los que normalmente suele hacer login a lo largo del día. Para ello vamos a realizar un análisis de un único usuario llamando “Neo” (originalidad ante todo chavales 😊). Para ello realizaremos la siguiente búsqueda.

index=wineventlog 4624 EventCode=4624 user=”neo”
| bucket _time span=1h 
| eventstats dc(Source_Network_Address) as "Uniq system logged into per user" by user _time 
| stats count by "Uniq system logged into per user"

Como veis, solo he filtrado los eventos 4624 (login exitoso en máquina) para mostrar mejor los datos y que se entienda más fácilmente. Bueno, a lo que vamos, ¿qué obtenemos con esto? La distribución del número de máquinas en las que nuestro usuario Neo suele hacer login durante el día en cajones de una hora. En otras palabras, representa que la mayoría de las veces (800), el usuario Neo ha hecho login en 2 máquinas cada día durante el tiempo en el que se ha realizado el estudio.

En modo tabla tendríamos:

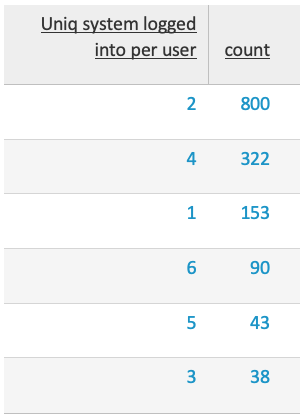
Como vemos, el número que más se repite es el 2. Bien, esto solo no nos dice nada… deberemos hallar la media, desviación típica y aplicar la fórmula de esta. No os voy a aburrir con matemáticas ahora más aún cuando lo hemos descrito en el apartado anterior. Splunk lo hace internamente y “no os tenéis que preocupar” por cómo se calcula. Eso sí, recomiendo encarecidamente que le echéis un ojo ya que no es una fórmula complicada y siempre viene bien repasar estos conceptos de las asignaturas de estadística de la carrera. Bueno, a lo que vamos. Para aplicar esto debemos añadir las siguientes líneas a nuestra búsqueda:

index=wineventlog 4624 EventCode=4624 user=”Neo"
| bucket _time span=1h
| eventstats dc(Source_Network_Address) as "Uniq system logged into per user" by user _time
| eventstats avg("Uniq system logged into per user") as "avg" by user
| eventstats stdev("Uniq system logged into per user") as "stdev" by user
| eval stdev=if('stdev'<1,1, stdev)
| eval upperBound=(avg+stdev*2) 
| eval isOutlier=if('Uniq system logged into per user' > upperBound, 1, 0) 
| where isOutlier=1
| transaction user _time
| table _time Source_Network_Address user "Uniq system logged into per user" upperBound avg stdev isOutlier

Esto generará la siguiente salida tal que esta:

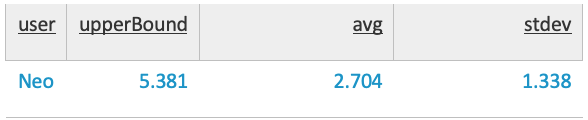
Aquí ya empezamos a ver cosas. Tenemos la media, la desviación típica y el límite superior o 2 veces σ. Acordaos, definimos como límite 2 veces la desviación típica. En este caso la desviación típica es 1,338 por lo que 2 * 1,338 nos dará 2,676. Si sumamos la media más dos veces la desviación típica obtendremos dicho límite. 2,704 + 2,676, efectivamente, 5,381.

Esto define el límite en el que un usuario puede logarse en diferentes equipos "sin llamar la atención” en nuestro correlador. Si dicho usuario en una hora determinada se loga en más de 5.381 equipos (6 o más máquinas) debemos generar una alerta. Hombre, no nos engañemos, siempre será más elegante aplicar un ceil() al upperbound y dejarlo en 6. Ceil lo que hace es redondear al número entero inmediatamente superior.

| eval upperBound=ceil((avg+stdev*2))

Ahora sólo debemos quedarnos con los eventos de la última hora (que es cuando se corre esta alerta, cada hora). Nótese que para que esta alerta tenga sentido, debemos calcular la media de logins que hacen los usuarios en un tiempo prudencial, es decir, debemos calcular la media y desviación típica en un tiempo prudente (una semana o 15 días) pero sólo alertar si en la última hora se ha generado una anomalía que exceda el límite superior calculado con los datos de esos 7 a 15 días. Finalmente, no queremos centrarnos sólo en nuestro querido usuario Neo; lo haremos extensible a todos los usuarios de la organización. Para ello basta con quitar el usuario de nuestro filtro el usuario en la búsqueda quedando algo así:

index=wineventlog 4624 EventCode=4624 user!=”*$”
| bucket _time span=1h
| eventstats dc(Source_Network_Address) as "Uniq system logged into per user" by user _time
| eventstats avg("Uniq system logged into per user") as "avg" by user
| eventstats stdev("Uniq system logged into per user") as "stdev" by user
| eval stdev=if('stdev'<1,1, stdev)
| eval upperBound=ceil((avg+stdev*2))
| eval isOutlier=if('Uniq system logged into per user' > upperBound, 1, 0) 
| where isOutlier=1
| transaction user _time
| table _time Source_Network_Address user "Uniq system logged into per user" upperBound avg stdev isOutlier

Nótese que he eliminado todas las cuentas que son de máquina (user!=”*$”) para evitar cálculos innecesario en el correlador. Ni que decir tiene que, si podéis afinar más la búsqueda de usuarios mejor que mejor, más limpiáis los datos y eso es trabajo que le ahorráis al search head de Splunk, además de evitar falsos positivos. La alerta sería similar a esta:

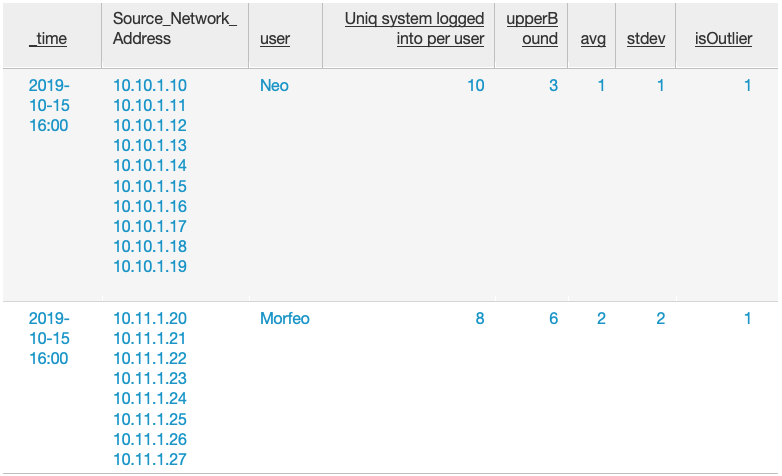
En la tabla anterior veríamos que, tanto el usuario Neo como el usuario Morfeo han contactado con un número de equipos (“Uniq system logged into per user”) mayor que su media más 2 veces su desviación típica. El flag “isOutlier” vale 1 sí se han cumplido las condiciones necesarias en la última hora. Se muestra además la lista de equipos en los que el usuario se ha logado.

Conclusiones

En aras de encontrar maneras no generalistas ni deterministas para aplicar nuevas alertas, hemos desarrollado nuevas fórmulas con las que adaptar a cada usuario el número válido de logins que suele hacer en diferentes máquinas. Esto aporta una personalización brutal dependiendo del comportamiento de cada usuario ya que no dependemos de una regla con un número determinado de logins sino que ajustaremos el umbral de manera estadística a cada usuario. Además, este tipo de casos de uso se puede trasladar a cualquier ámbito de la seguridad. Si nos ponemos en modo paranoico, podremos:

• Modelar el número de IPs con los que cada máquina suele comunicar cada día. Un usuario, normalmente, contactará con un número determinado de máquinas dentro de su organización (proxy, servidor de correo, sharepoint, nas, etc.). Si hay un aumento en el número de host con los que una máquina suele contactar, podría ser indicio de potencial escaneo de equipos. Usaríamos logs de firewalls para esto.
• Modelar el número de puertos destino con los que cada IP suele conectar. Si un usuario suele conectar con 30 puertos diferentes normalmente (25, 53, 139, 80, 443, 8080, etc) y un día hay un incremento grande, potencial escaneo de puertos. Usaríamos logs de firewalls para esto.
• Detectar cuando un usuario genera de manera sostenida eventos de seguridad en el antivirus. Esto podría suponer un riesgo ya que el usuario está ejecutando o descargando software malintencionado poniendo en riesgo la organización.

El resto, dejar volar vuestra imaginación y aplicarlo a datos en los que pueda encajar este tipo de aproximaciones estadísticas.